以Java實作最簡單版本的Neural Network

July 25, 2015 | 2 Minute Read

最近因為Deep Learning話題挺多的，所以稍微研究一下它的前身Neural Network。剛好看到了這篇文章A Neural Network in 11 lines of Python，想說試著用Java寫寫看。原本想說在這邊做一些NN的推導說明，但是實在太難用一篇Blog解釋了(呈現懶惰狀態)。所以先假設讀者了解Neural Network最基本概念，跟最基本的Training方式。若不瞭解可以聽聽台大林軒田老師在Coursera平台上面的講課內容，裡面有一章Neural Network，非常值得一看。

話不多說，先給我最後的程式碼。

給我程式碼

可以直接到Github下載，或是Fork出去。

package idv.popcorny.nnet;

import org.la4j.Matrix;
import java.util.Random;

/**
 * The code was inspired by http://iamtrask.github.io/2015/07/12/basic-python-network/
 */
public class SimpleNNet {
    public static void main(String[] args) {
        Matrix X = Matrix.from2DArray(new double[][]{
                {0, 0, 1},
                {0, 1, 1},
                {1, 0, 1},
                {1, 1, 1},
        });
        Matrix Y = Matrix.from2DArray(new double[][]{
                {0, 1, 1, 0}
        }).transpose();

        Random random = new Random();
        Matrix Syn0 = Matrix.random(3, 4, random)
                .multiply(2)
                .subtract(1);
        Matrix Syn1 = Matrix.random(4, 1, random)
                .multiply(2)
                .subtract(1);

        Matrix X0 = X;
        Matrix X1 = null;
        Matrix X2 = null;
		for (int loop=1; loop<=50000; loop++) {
            // Forward
            // s1 = x0 . syn0
            // x1 = sigmoid(s1)
            Matrix S1 = X0.multiply(Syn0);
            X1 = S1.transform((i, j, value) -> sigmoid(value));
            // s2 = x1 . syn1
            // x2 = sigmoid(x1 . syn1)
            Matrix S2 = X1.multiply(Syn1);
            X2 = S2.transform((i, j, value) -> sigmoid(value));

            // Backward
            // l2_delta = 2*(y - x2)*sigmoid'(s2)
            Matrix L2_delta = Y.subtract(X2).multiply(2).hadamardProduct(
                S2.transform((i, j, value) -> sigmoid_deriv(value))
            );

            // l1_delta = l2_delta.dot(syn1.T) * sigmoid'(s1)
            Matrix L1_delta = L2_delta.multiply(Syn1.transpose()).hadamardProduct(
                S1.transform((i, j, value) -> sigmoid_deriv(value))
            );

            // Update the weights
            // syn1 += x1.T.dot(l2_delta)
            Syn1 = Syn1.add(X1.transpose().multiply(L2_delta));
            // syn0 += X.T.dot(l1_delta)
            Syn0 = Syn0.add(X0.transpose().multiply(L1_delta));
        }

        System.out.println(X2);
    }

    /**
     * Sigmoid Function: https://en.wikipedia.org/wiki/Sigmoid_function
     */
    private static double sigmoid(double x) {
        return 1 / (1 + Math.exp(-x));
    }

    /**
     * Derivation of Sigmoid Function: https://en.wikipedia.org/wiki/Sigmoid_function
     */
    private static double sigmoid_deriv(double x) {
        return sigmoid(x) * (1 - sigmoid(x));
    }
}

執行方法(需要Java8)

./gradlew run

最後出來的結果會是

一定會有人說怎麼比Python版本多那麼多程式碼，因為我有註解啊!! 不過當然我知道是藉口 XD，即使去掉註解，還是比Python多上許多行，這點我最後再來討論這方面的話題。

詳解

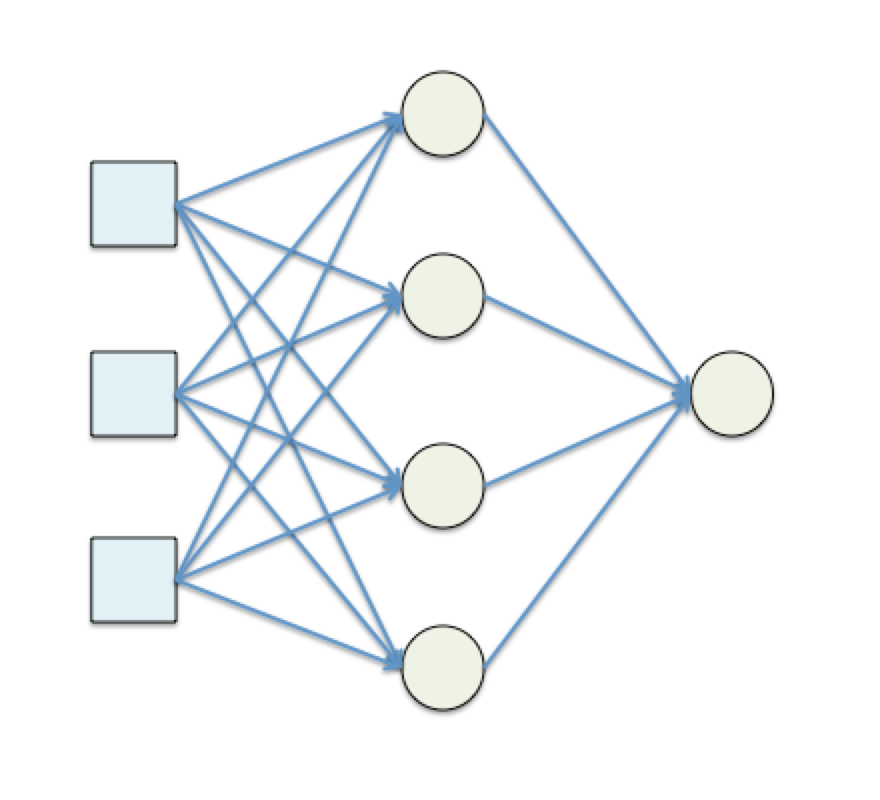
首先這是一個3-4-1 Neural Network。也就是Input Layer有3個Dimensions；中間只有一個Hidden Layout，並且為4個Dimensions；最後Output Layer為1個Dimensions。每個Neural都是用Sigmoid function當作Activation Function。所以整個Neural Network會長成這樣。

再來是變數解釋

Variable	Description
X	Input Data
Y	Output Data
X0,X1,X2	每一層的Outputs，也是下一層的Input。所以X0 = X。
SYN0,SYN1	Synapse(突觸)，也就是每一層的Weights。SYN0是一個3x4的矩陣，SYN1是一個4x1的矩陣。分別也代表著Layer0到Layer1的連線，跟Layer1到Layer2的連線。
S1,S2	為每個Neural針對某一個連線的linear combination。也就是S1 = X0 dot SYN0
L1_Delta, L2_Delta	為Back Propragation所用的中間變數。

再來是程式碼解釋。首先我使用了la4j這個Library，因為Machine Learning裡面用了非常多的線性代數，而la4j是一個線性代數的Library。使用的主要是矩陣運算。

逐行解釋，建議開兩個瀏覽器視窗來交叉參照。

line11 ~ 19: 這邊我準備了4個input/output

Inputs	Output
(0, 0, 1, 1)	0
(0, 1, 1, 1)	1
(1, 0, 1, 1)	1
(1, 1, 1, 1)	0

line21~27: 把每個Weights都設定初始值。隨機的設定範圍在(-1, 1)之間的值。
line32: 開始做50000次的iteration
line36~41: Forward(Predcit)的部分，這部分很單純，就是把前一層的Input經過每一條連線乘上Weight，並且在Neural上面加總起來。並且最後經過一個Sigmoid function做轉換輸出。事實上對於有學過Logistic Regression的人來講，每一個Node基本上都是一個Logistic Regression Model。所以對一個Neural的表示法是這樣
```
output =  sigmoid(w0x0 + w1x1 + w2x2 + ...)
```
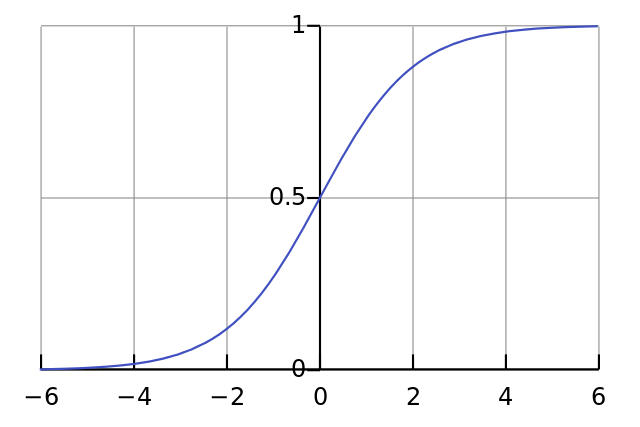
而Sigmoid Function的圖形會長這樣，目的就是希望達到正無限大的時候是1，負無限大的時候是0，而當input是0的時候剛好是0.5。Sigmoid Function最常拿來把實數空間來轉到(0,1)之間，方便來描述機率。

在一層一層傳遞後，最後的Output Layer就會輸出一個結果出來。因為也是透過Sigmoid，所以Output結果也是(0,1)之間。
line43~52: 為Backward Propagation。在Neural Network重點當然是學習，而學習就是要從錯誤中學習，所以我們要先定義什麼叫做錯誤。最簡單的錯誤的衡量方法是Mean Square Error也就是把目前答案跟正確答案相減取平方E = (y - x2)^2，有些時候我們也會稱錯誤衡量所用的韓式稱為Loss Function。再來是使用梯度下降法Gradient Descent的方式來讓每個Iteration的錯誤減少。此方法是對每個維度去做梯度下降，如果一個某個函數的呈現是會有一個谷底的，那麼最底端的梯度，也就是對每一個維度的偏微分應該為0。所以我們會針對每個點找出他的梯度向量，並且反方向走一步，來達到每個iteration的梯度下降。在類神經網路，每一條線上面的weight就是一個維度，所以這個梯度就是要對每個weight去做偏微分，聽起來好像有點困難，但是可以推導出這個偏微分可以透過Back Propagation的方式算出。
line45~47: 對最後一層的weights去做偏微分。因為最後一層的Weights跟最後的Loss Function比較近。我們可以很容易的算出偏微分函示如以下所示:
```
E = (y - x2)^2 = (y - sigmoid(S2))^2
=>
dE/dw  = dE/dS2 * dS2/dw
dE/dS2 = -2(y - sigmoid(S2)) * sigmoid`(S2)
     = -2(y - S2) * sigmoid`(S2)
dS2/dw = x
```
而L2_delta就是dE/dS，只是因為我們會往回走，所以負號就剛好消掉，這個會在之後backprop傳遞給前一層。而dS/dw就是前一層該link的input，也就是X1的某個output。

程式碼中的Multiply跟
hadamardProduct需要解釋一下。前者是我們常見的兩個矩陣相乘，後者是兩個矩陣中同樣位置的item兩兩相乘。
line50~52: 就是對再前層的weights去做偏微分，這邊根據推導(這邊請看林老師的教學)會得到以下結果。
```
dE/dw  = dE/dS1 * dS/dw
dE/dS1 = dE/dS2 dot Syn1 * sigmoid`(S1)
dS/dw  = x
```
也就是delta_l1是透過delta_l2推導過來的，這就是Neural Network的back propagation。
line56~58: 最後針對梯度向量反方向，走一步。實務上來講，我們還會給一定一個η來決定走的距離。可以想像梯度代表的是方向盤，η代表的是油門。這個油門太大可能不容易收斂，η太小就會學得比較慢。這是需要去調控的。
line64~: 就是Sigmoid function跟他的一次微分。

討論

其實我自己常常覺得有些東西沒有自己動手做就沒有感覺，而這篇的目的就是希望用一個Java檔，就可以實作一個最簡單版的Neural Network。從Forward到Backprop，到多個Iteration，最後可以收斂到一個可以用的結果。我希望各位也可以動手玩玩看，因為NN看起來真的很Magic，如果只是把它當作黑盒子使用，我覺得不能體會到他的精髓。而且我相信很多人跟我一樣，再多的公式比不上一段程式，程式比文件更具說服力。

另外其實NN很有彈性。像我們用的Sigmoid Function當作Activation Function，事實上更常用的可能是Hyperbolic Tangent。還有最後的Loss Function也可以換成Cross Entropy Loss Function，這對機率類型的評估會比較合理一些。而NN中間很多層的Hidden Layer就是Deep Learning。至於Topology也可能有很多種變形，來針對不同的問題來做調整。

另外NN還有一些要注意，那就是NN是一個非常Powerful的Model，但是太Powerful，就是容易Overfitting。所以最好還是要搭配一些Regularization的方法，或是Early Stopping的方式來避免。

還有NN還有一個不知道算不算嚴重的問題(抱歉這方面我比較不清楚)，就是Gradient Descent對於會有Local minimum的function會不小心困在Local Minimum而無法到達Global Minimum。這點可能有一些方法可以稍微避免這個問題，這點我就比較沒有經驗了。

最後前面提到Java實作怎麼那麼複雜。Java是囉唆的語言著稱(笑)，Java本身沒有支援Operation Overloading)，這點對於這種一堆數學運算真的很不方便。相對的Python就好很多，其實好像現在要找到不支援Operation Overloading的語言還真的不多(再笑)。如果要在JVM上面開發類似的應用，也許Scala會好一點。

« 在github pages上面使用jekyll架設部落格

Popcorny的碎碎唸

以Java實作最簡單版本的Neural Network

給我程式碼

詳解

討論